Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The circumference of two circles are in ratio 2:3. Find the ratio of their areas
рдЙрддреНрддрд░
Let radius of two circles be ЁЭСЯ1 and ЁЭСЯ2 then their circumferences will be 2ЁЭЬЛЁЭСЯ1 : 2ЁЭЬЛЁЭСЯ2
= ЁЭСЯ1: ЁЭСЯ2
But circumference ratio is given as 2 : 3
ЁЭСЯ1: ЁЭСЯ2 = 2: 3
Ratio of areas = ЁЭЬЛЁЭСЯ22: ЁЭЬЛЁЭСЯ22
`= (r_1/r_2)^2`
`=(12/3)^2`
`= 4/9`
= 4:9
∴ ЁЭСЯЁЭСОЁЭСбЁЭСЦЁЭСЬ ЁЭСЬЁЭСУ ЁЭСОЁЭСЯЁЭСТЁЭСОЁЭСа = 4 тИ╢ 9
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
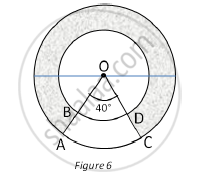
In Fig. 6, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. (use `pi = 22/7`)
A car travels 1 km distance in which each wheel makes 450 complete revolutions. Find the radius of wheel.
The area of a minor sector of a circle is 3.85 cm2 and the measure of its central angle is 36°. Find the radius of the circle.
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
The perimeter of the quadrant of a circle is 25 cm. Find its area.
Find the diameter of the sphere for the following :
Volume = `523 17/21` cm3
The sum of the circumference and diameter of a circle is 116 cm. Find its radius.
An express train is running between two stations with a uniform speed. If the diameter of each wheel of the train is 42 cm and each wheel makes 1200 revolutions per minute, find the speed of the train.
Circumference of a circle is always ______.
The moon is about 384000 km from earth and its path around the earth is nearly circular. Find the length of path described by moon in one complete revolution. (Take π = 3.14)
