Advertisements
Advertisements
प्रश्न
The moon is about 384000 km from earth and its path around the earth is nearly circular. Find the length of path described by moon in one complete revolution. (Take π = 3.14)
उत्तर
Length of path described by moon in one complete revolution = 2πr
= 2 × 3.14 × 384000 ......[∵ Radius = Distance of moon from the earth]
= 2411520 km
APPEARS IN
संबंधित प्रश्न
A race track is in the form of a ring whose inner circumference is 352 m, and the outer circumference is 396 m. Find the width of the track.
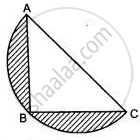
ABC is an isosceles right-angled triangle with ∠ABC = 90°. A semi-circle is drawn with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region. [Take π = 22/7]
Find the area of the rhombus, the length of whose diagonals are 30 cm and 16 cm. Also, find the perimeter of the rhombus.
The difference between the circumference and radius of a circle is 37cm. Using `pi = 22/7` , find the circumference of the circle.
The circumference of a circle is equal to the sum of the circumference of two circles having diameters 36 cm and 20 cm. The radius of the new circle is
Find the area and perimeter of the following semi-circle :
Radius= 1.4 cm
A wheel has a diameter of 84 cm. Find how many completer revolutions must it make to cover 3.168 km.
Using a ruler and compasses only:
(i) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ ABC = 120°.
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠ BCP.
What is the circumference of a circle of diameter 10 cm (Take π = 3.14)?
Find the circumference of the circles whose radii are given below.
91 mm
