Advertisements
Advertisements
प्रश्न
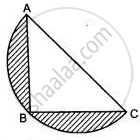
ABC is an isosceles right-angled triangle with ∠ABC = 90°. A semi-circle is drawn with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region. [Take π = 22/7]
उत्तर
In ΔABC, using Pythagoras theorem
AC2 = AB2 + BC2
AC2 = (7)2 + (7)2
AC2 = 49 + 49
AC2 = 98
⇒ AC = `7sqrt2`
Radius of semi-circle = `"AC"/2 = (7sqrt2)/2`
∴ Area of the shaded region = Area of semi-circle – Area of ΔABC
Area of semi-circle = `1/2 pir^2 = 1/2 pi((7sqrt2)/2)^2`
= `(98pi)/8 = (49pi)/4`
= `49/4`
= `49/4 xx 22/7`
= `77/2 "cm"^2`
Area of ΔABC = `1/2` x BC x AB
= `1/2` x 7 x 7
= `49/2 "cm"^2 `
Thus, Area of the shaded region = `77/2 "cm"^2 - 49/2 "cm"^2 = 28/2 "cm"^2 = 14 "cm"^2`.
APPEARS IN
संबंधित प्रश्न
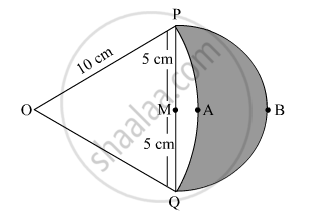
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.
In Fig. there are shown sectors of two concentric circles of radii 7 cm and 3.5 cm. Find the area of the shaded region. Use π = `(\frac { 22 }{ 7 }).`
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
An arc of length 20𝜋 cm subtends an angle of 144° at centre of circle. Find the radius of the circle.
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
The circumferences of two circles are in the ratio 2: 3. What is the ratio between their areas?
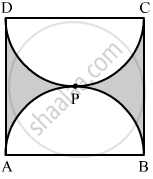
Find the perimeter of the shaded region in the figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles.
The circumference of a circle is 39.6 cm. Find its area.
The wheels of a car make 2500 revolutions in covering a distance of 4.95 km. Find the diameter of a wheel.
In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre. If `sqrt(3) = 1.73` then the area of the segment of the circle is
The speed of the car is 66 km/hour. If each wheel of the car is 140 cm in diameter, find the number of revolutions made by each wheel per minute.
The cost of fencing a circular field at the rate of ₹ 240 per meter is ₹ 52,800. The field is to be ploughed at the rate of ₹ 12.50 per m2. Find the cost of pouching the field.
There are two circular gardens A and B. The circumference of garden A is 1.760 km and the area of garden B is 25 times the area of garden A. Find the circumference of garden B.
The circumference of a circle exceeds its diameter by 18 cm. find the radius of the circle.
Find the area and perimeter of the following semicircles: Radius = 1.4cm
The area between the circumference of two concentric circles is 2464cm2. If the inner circle has a circumference of 132cm, calculate the radius of the outer circle.
What is the circumference of a circle of diameter 10 cm (Take π = 3.14)?
Sudhanshu divides a circular disc of radius 7 cm in two equal parts. What is the perimeter of each semicircular shape disc? (Use π = `22/7`)
Find the area of the shaded region given in figure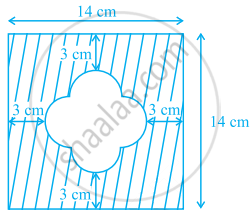
Ratio of the circumference of a circle to its diameter is denoted by symbol ______.
