Advertisements
Advertisements
प्रश्न
Find the area of the shaded region given in figure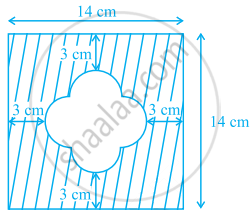
उत्तर
ABCD is a square of side 14 cm.
Join JK, KL, LM and MJ.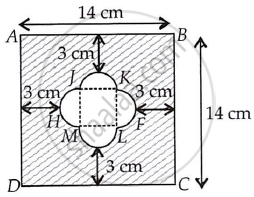
There are four equal semi-circles and JKLM formed a square.
∴ FH = 14 – (3 + 3) = 8 cm
So, the side of square JKLM is 4 cm and radius of semi-circle of both ends are 2 cm each.
∴ Area of square JKLM = (4)2 = 16 cm2
Area of semi-circle HJM = `(π"r"^2)/2`
= `(π xx (2)^2)/2`
= 2π cm2
∴ Area of four semi-circles
= 4 × 2π
= 8π cm2
Now, area of square ABCD = (14)2 cm2 = 196 cm2
∴ Area of shaded region = Area of square
ABCD – [Area of four semi-circles + Area of square JKLM]
= 196 – [8π + 16]
= 196 – 16 – 8π
= (180 – 8π) cm2
Hence, the required area of the shaded region is (180 – 8π) cm2.
APPEARS IN
संबंधित प्रश्न
A sheet of paper is in the form of rectangle ABCD in which AB = 40cm and AD = 28 cm. A semicircular portion with BC as diameter is cut off. Find the area of remaining paper.
Diagonal of a square is 20 cm. Find the length and perimeter of the square.
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr ?
A sector of 56°, cut out from a circle, contains 17.6 cm2. Find the radius of the circle.
Find the area of a quadrant of a circle whose circumference is 88 cm.
Find the area and perimeter of the circle with the following:
Diameter= 35 cm
If the circumference of a circle is 176 cm, find its radius.
Find the area and perimeter of the circles with following: Diameter = 77cm
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 28 mm
A ground is in the form of a circle whose diameter is 350 m. An athlete makes 4 revolutions. Find the distance covered by the athlete
