Advertisements
Advertisements
प्रश्न
Find the area and perimeter of the following semi-circle :
Radius= 1.4 cm
उत्तर
Area of the semi-circle = `1/2 pi "r"^2`
`= 1/2 xx 22/7 xx 1.4 xx 1.4`
= 3.08 cm2
Perimeter of the semi-circle = (πr + 2r)
`= (22/7 xx 1..4) + (2 xx 1.4)`
= 7.2 cm
Therefore, Area= 3.08 cm2 and Perimeter= 7.2 cm.
APPEARS IN
संबंधित प्रश्न
Find the circumference of the circle with the following radius: (Take `bb(pi = 22/7`)
14 cm
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the costs of the rope, if it cost ₹ 4 per meter. (Take `pi = 22/7`)
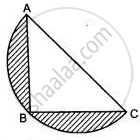
ABC is an isosceles right-angled triangle with ∠ABC = 90°. A semi-circle is drawn with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region. [Take π = 22/7]
The circumference of a circle exceeds diameter by 16.8 cm. Find the circumference of
circle.
A steel wire when bent is the form of square encloses an area of 12 cm2. If the same wire is bent in form of circle. Find the area of circle.
A horse is placed for grazing inside a rectangular field 40m by 36m and is tethered to one corner by a rope 14m long. Over how much area can it graze.
The shape of the cross section of a canal is a trapezium. If the canal is 10 m wide at the top, 6 m wide at the bottom and the area of its cross section is `640m^2` , find the depth of the canal.
The circumference of a circle is 8 cm. Find the area of the sector whose central angle is 72°.
A canvas tent is in the shape of a cylinder surmounted by a conical roof. The common diameter of the cone and the cylinder is 14 m. The height of the cylindrical part is 8 m and the height of the conical roof is 4 m. Find the area of the canvas used to make the tent.
The diameter of a circle is 28 cm.
Find its :
(i) Circumference
(ii) Area.
The circumference of a circle is 440 cm. Find its radius and diameter. (Take π = `22/7`)
Using a ruler and compasses only:
(i) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ ABC = 120°.
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠ BCP.
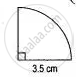
In the adjoining figure, the radius is 3.5 cm. Find:
(i) The area of the quarter of the circle correct to one decimal place.
(ii) The perimeter of the quarter of the circle correct to one decimal place. ( Take π = `22/7`)
The diameter of two circles are 28 cm and 24 cm. Find the circumference of the circle having its area equal to sum of the areas of the two circles.
A wire when bent in the form of a square encloses an area of 484cm2. If the same wire is bent into the form of a circle, find the area of the circle.
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 56 m
The perimeter of a sector of radius 5.2 cm is 16.4 cm, the area of the sector is ____________.
Circumferences of two circles are equal. Is it necessary that their areas be equal? Why?
The area of a circular playground is 22176 m2. Find the cost of fencing this ground at the rate of Rs 50 per metre.
A wire is bent to form a square of side 22 cm. If the wire is rebent to form a circle, its radius is ______.
