Advertisements
Advertisements
рдкреНрд░рд╢реНрди
A horse is placed for grazing inside a rectangular field 40m by 36m and is tethered to one corner by a rope 14m long. Over how much area can it graze.
рдЙрддреНрддрд░
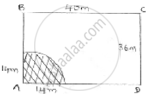
The fig shows rectangular field ABCD at corner A, a horse is tied with rope length = 14m.
The area it can graze is represented A as shaded region= area of quadrant with (radius = length) of string
Area = `1/4`× (ЁЭСОЁЭСЯЁЭСТЁЭСО ЁЭСЬЁЭСУ ЁЭСРЁЭСЦЁЭСЯЁЭСРЁЭСЩЁЭСТ) = ЁЭЬЛЁЭСЯ2
`= 1/4 ×22/7 × 14 × 14`
= (22 × 7)
= 154 m2.
Area it can graze = 154m2.
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
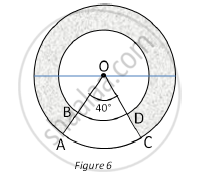
In Fig. 6, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. (use `pi = 22/7`)
The radii of two concentric circles are 19 cm and 16 cm respectively. The area of the ring enclosed by these circles is
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the area of the minor and major segments.
Find the area and perimeter of the circle with the following :
Radius= 2.8 cm
A wire is in the form of a circle of radius 42 cm. It is bent into a square.
Determine the side of the square and compare the area of the regions enclosed in two cases.
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has a circumference equal to the sum of circumferences of these two circles.
Find the area and perimeter of the following semicircles: Diameter = 5.6cm
A cart wheel makes 9 revolutions per second. If the diameter of the wheel is 42cm, find its speed in km per hour. (Answer correct to the nearest km)
The circumference of a circle is equal to the perimeter of a square. The area of the square is 484 sq.m. Find the area of the circle.
Circumferences of two circles are equal. Is it necessary that their areas be equal? Why?
