Advertisements
Advertisements
प्रश्न
The area of a square is the same as the area of a square. Their perimeters are in the ratio
विकल्प
1 : 1
2 : π
π : 2
`sqrt(pi):2`
उत्तर
`sqrt(pi): 2`
Let a be the side of the square.
We know:
Area of a square = a2
Let r be the radius of the circle.
We know:
Area of a circle`=pi"r"^2`
Because the area of the square is the same as the area of the circle, we have:
a2 = πr2
`=> "r"^2/"a"^2 = 1/pi`
`=>"r"/"a" = 1/sqrt(pi)`
∴ Ratio of their perimeters
`=(2pi"r")/(4"a") ["Because perimeter of the circle is 2πr and permeter" "of the square is 4"a"]`
`=(pi"r")/(2"a")`
`=pi/2xx"r"/"a"`
`=pi/2xx1/sqrt(pi) ["Since" "r"/"a" = 1/sqrt(pi)]`
`=sqrt(pi)/2`
`= sqrt(pi) : 2`
APPEARS IN
संबंधित प्रश्न
In figure, ΔABC is an isosceles triangle with perimeter 44 cm. The base BC is of length 12 cm. Side AB and side AC are congruent. A circle touches the three sides as shown in the figure below. Find the length of the tangent segment from A to the circle.
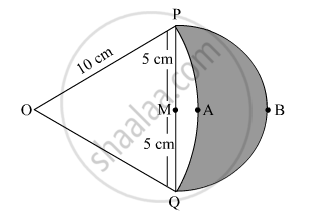
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.
The circumference of a circle exceeds the diameter by 16.8 cm. Find the radius of the circle.
The inner circumference of a circular track is 220 m. The track is 7m wide everywhere. Calculate the cost of putting up a fence along the outer circle at the rate of j – 2 per metre. (Use π = 22/7)
The circumference of a circle exceeds its diameter by 45 cm. Find the circumference of the circle.
The side of a square is 10 cm. Find the area of the circumscribed circle. [π = 3.14]
The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the perimeter of the triangle.
Complete the table below.
| Radius (r) | Diameter (d) | Circumference (c) |
| ...... | ...... | 72.6 cm |
Length of tape required to cover the edges of a semicircular disc of radius 10 cm is ______.
Circumference ‘C’ of a circle is equal to 2π × ______.
