Advertisements
Advertisements
Question
Find the angle subtended at the centre of circle of radius 5cm by an arc of length `((5pi)/3)` cm
Solution
Radius (r) = 5 cm
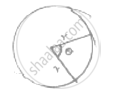
𝜃 = angle subtended at centre (degrees)
Length of Arc =`theta/360^@`× 2𝜋r cm
But arc length =`5pi/3`𝑐𝑚
`theta/360^@× 2pi × 5 =(5pi)/3`
`theta=(360^@×pi)/(3×2pi)= 60^@`
∴ Angle subtended at centre = 60°
APPEARS IN
RELATED QUESTIONS
In Figure, find the area of the shaded region [Use π = 3.14]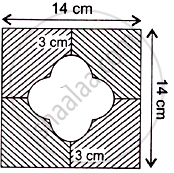
If the perimeter of a semi-circular protractor is 66 cm, find the diameter of the protractor (Take π = 22/7).
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
The hypotenuse of a right-angled triangle is 65 cm and its base is 60 cm. Find the length of perpendicular and the area of the triangle.
Find the diameter of the circle whose area is equal to the sum of the areas of two circles having radii 4 cm and 3 cm.
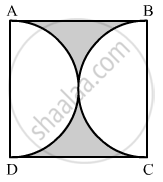
In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
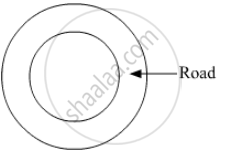
Diameter of the circular garden is 42 m. There is a 3.5 m wide road around the garden. Find the area of the road.
Construct an angle PQR = 45°. Mark a point S on QR such that QS = 4.5 cm. Construct a circle to touch PQ at Q and also to pass through S.
The center O of a circle of a radius 1.3 cm is at a distance of 3.8 cm from a given straight line AB. Draw a circle to touch the given straight line AB at a point P so that OP = 4.7 cm and to touch the given circle externally.
Value of π is ______ approximately.
