Advertisements
Advertisements
प्रश्न
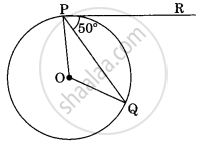
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

उत्तर

Given, ∠ABO = 40°
∠XAO = 90° ...(Angle between radius and tangent)
OA = OB ...(Radii of same circle)
⇒ ∠OAB = ∠OBA
∴ ∠OAB = 40°
Now, applying the linear pair of angles property,
we get
∠BAY + ∠OAB + ∠XAO = 180°
⇒ ∠BAY + 40° + 90° = 180°
⇒ ∠BAY + 130° = 180°
⇒ ∠BAY = 180° – 130°
⇒ ∠BAY = 50°
Now, In ΔAOB,
∠AOB + ∠OAB + ∠OBA = 180°
or, ∠AOB + 40° + 40° = 180°
or, ∠AOB = 180° – 80° = 100°
APPEARS IN
संबंधित प्रश्न
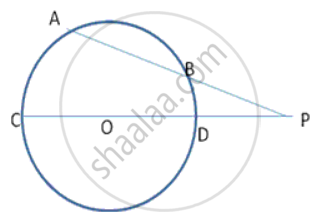
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
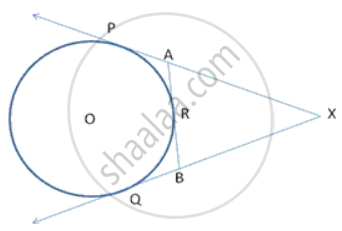
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

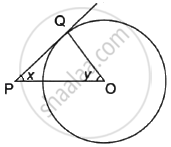
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.