Advertisements
Advertisements
Question
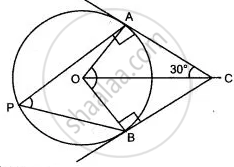
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
Solution
(i) ∠ BCO = ∠ ACO = 30° .....( ∴ C is the intersecting point of tangents AC and BC)
(ii) ∠ OAC = ∠ OBC = 90°
∠ ACO = 30° .....(Given)
∠ AOC = ∠ BOC = 180° - (90° + 30°) ....(Sum of the angles of a Δ is 180°)
∠ AOC = 180° - 120°
∠ AOC = 60°
∠ AOB = ∠ AOC + ∠ BOC
∠ AOB = 60° + 60° = 120°
(iii) ∠ APB = `1/2"∠ AOB" = (120°)/2 = 60°` .....( ∴ Angle substended at the remaining part of the circle is half the ∠ substended at the centre)
APPEARS IN
RELATED QUESTIONS
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
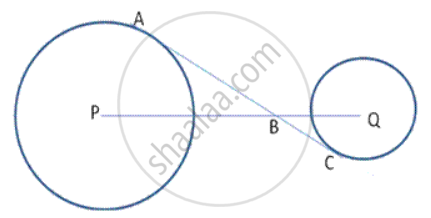
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
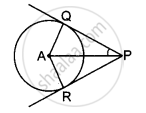
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
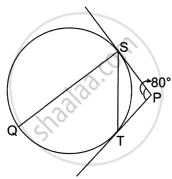
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
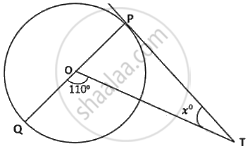
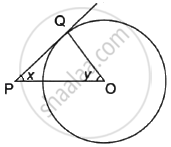
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.