Advertisements
Advertisements
Question
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution 1
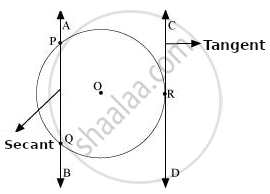
- It can be observed that AB and CD are two parallel lines. Line AB intersects the circle at exactly two points, P and Q.
- Therefore, line AB is the secant of this circle. Since line CD is intersecting the circle at exactly one point, R, line CD is the tangent to the circle.
Solution 2
We have the required figure, as shown.
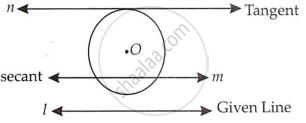
Here, I represents the given line, and a circle with center O is drawn. Another line, m is drawn parallel to l and acts as a tangent to the circle. Additionally, line m, which is also parallel to is drawn as a secant to the circle.
APPEARS IN
RELATED QUESTIONS
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
How many tangents can a circle have?
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
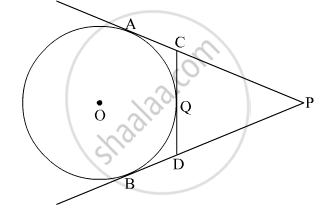
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
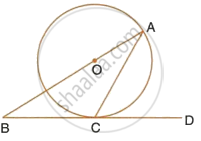
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.
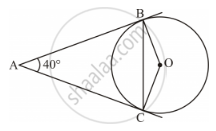
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
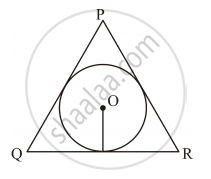
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
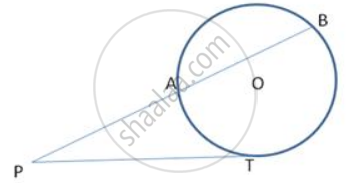
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
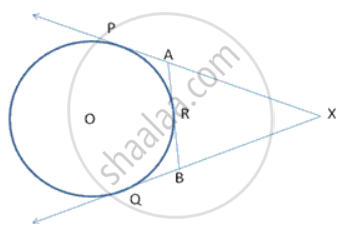
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.