Advertisements
Advertisements
Question
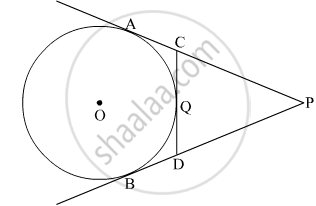
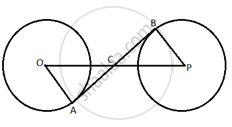
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
Solution
Given: PA and PB are the tangents to the circle.
PA = 12 cm
QC = QD = 3 cm
To find: PC + PD
PA = PB = 12 cm (The lengths of tangents drawn from an external point to a circle are equal)
Similarly, QC = AC = 3 cm and QD = BD = 3 cm.
Now, PC = PA − AC = 12 − 3 = 9 cm
Similarly, PD = PB − BD = 12 − 3 = 9 cm
Hence, PC + PD = 9 + 9 = 18 cm.
APPEARS IN
RELATED QUESTIONS
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

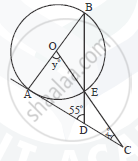
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

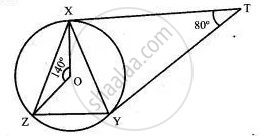
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.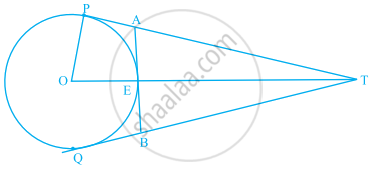
How many tangents can be drawn to a circle from a point on it?
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
