Advertisements
Advertisements
प्रश्न
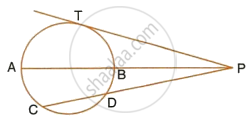
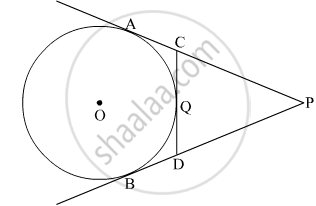
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
उत्तर
Given: PA and PB are the tangents to the circle.
PA = 12 cm
QC = QD = 3 cm
To find: PC + PD
PA = PB = 12 cm (The lengths of tangents drawn from an external point to a circle are equal)
Similarly, QC = AC = 3 cm and QD = BD = 3 cm.
Now, PC = PA − AC = 12 − 3 = 9 cm
Similarly, PD = PB − BD = 12 − 3 = 9 cm
Hence, PC + PD = 9 + 9 = 18 cm.
APPEARS IN
संबंधित प्रश्न
A line intersecting a circle in two points is called a ______.
Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
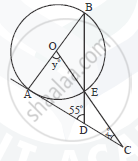
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
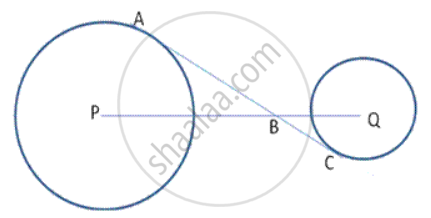
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
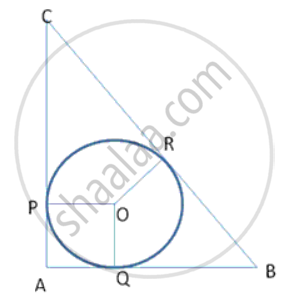
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.