Advertisements
Advertisements
प्रश्न
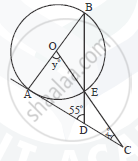
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
उत्तर
In ΔABD, ∠BAD = 90°
∴ ∠ABD + ∠BAD + ∠ADB = 180° {Sum of angles in a triangle}
∴ ∠ABD + 90° + 55° =180°
∴ ∠ABD = 35°
Also ∠AOE = 2∠ABE = 2∠ABD
∴ ∠AOE = y = 2 × 35°
| y = 70° |
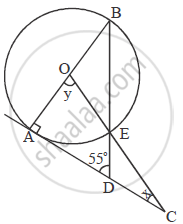
In Δ AOC,
∠OAC + x + y = 180°
∴ 90° + x + 70° = 180°
∴ 90° + x + 70° = 180°
| ⇒ x = 20° |
APPEARS IN
संबंधित प्रश्न
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
How many common tangents can be drawn to two circles, touching each
other externally?
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
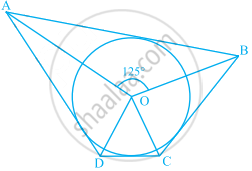
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
The tangents drawn at the extremities of the diameter of a circle are ______.
The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______