Advertisements
Advertisements
प्रश्न
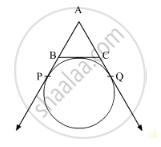
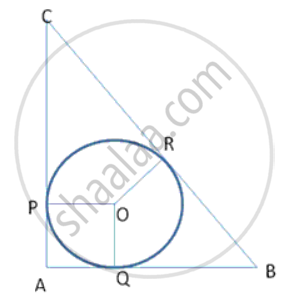
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
विकल्प
A. 7.5
B. 15
C. 10
D. 9
उत्तर
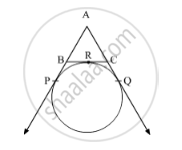
AP, AQ and BC are tangents to the circle. Suppose BC touch the circle at R.
It is given that AB = 5 cm, AC = 6 cm and BC = 4 cm.
We know that, the lengths of tangents drawn from an external point to a circle are equal.
∴ AP = AQ … (1)
PB = BR … (2)
CQ = CR .... (3)
2AP = AP + AP
∴ 2AP = AP + AQ [Using (1)]
⇒ 2AP = (AB + PB) + (AC + CQ)
⇒ 2AP = (AB + BR) + (AC + CR) [Using (2) and (3)]
⇒ 2AP = AB + (BR + CR) + AC
⇒ 2AP = AB + BC + AC
⇒ 2AP = 5 cm + 4 cm + 6 cm
⇒ 2AP = 15 cm
⇒ AP = 7.5 cm
Thus, the length of AP is 7.5 cm.
Hence, the correct answer is A.
APPEARS IN
संबंधित प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

The common point of a tangent to a circle and the circle is called ______.
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
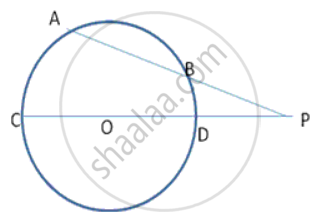
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
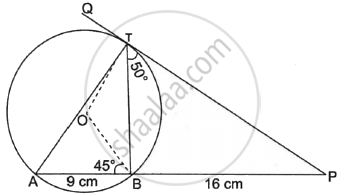
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT