Advertisements
Advertisements
प्रश्न
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
उत्तर
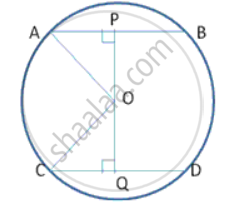
AP = PB = 3cm
CQ = QD = 6cm (Perpendicular from centre to a chord bisects the chord)
OA = OC = r (say)
Let OP = x, ∴ OQ = 3 - x
In right Δ OQC,
By Pythagoras theorem,
OC2 = OQ2 + CQ2
r2 = (3-x)2 + 62 ----(1)
Similarly, In Δ OPA,
OA2 = AP2 + PO2
r2 = 32 + x2 ----(2}
From (1) and {2}
(3-x)2 + 62 = 32+ x2
-6x + 36 = 0
x = 6
from {2}
r2 = 32 + 62 = 9 + 36 = 45
r = `3 sqrt 5`
Thus , radius of the circle is `3 sqrt 5` cm
APPEARS IN
संबंधित प्रश्न
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
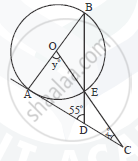
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
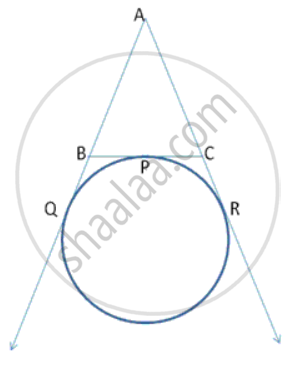
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

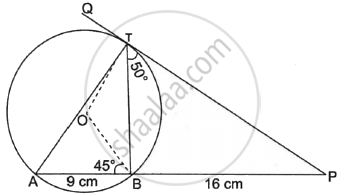
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

