Advertisements
Advertisements
प्रश्न
Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5
उत्तर
Steps of construction:
1) Draw a line segment AB = 8 cm.
2) Draw a ray AX making an acute angle ∠BAX=60° with AB.
3) Draw a ray BY parallel to AX by making an acute angle ∠ABY = ∠BAX.
4) Mark four points A1, A2, A3, A4 on AX and five points B1,B2,B3,B4,B5 on BY in such a way that AA1=A1A2=A2A3=A3A4.
5) Join A4B5
6) Let this line intersect AB at a point P.
Thus, P is the point dividing the line segment AB internally in the ratio of 4 : 5.

APPEARS IN
संबंधित प्रश्न
Determine a point which divides a line segment of length 12 cm internally in the ratio 2 : 3 Also, justify your construction.
Divide a line segment of length 14 cm internally in the ratio 2 : 5. Also, justify your construction.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are \[\frac{3}{5}\] times the corresponding sides of the given triangle.
Choose the correct alternative:

In the figure ΔABC ~ ΔADE then the ratio of their corresponding sides is ______
Construct an equilateral ∆ABC with side 5 cm. ∆ABC ~ ∆LMN, ratio the corresponding sides of triangle is 6 : 7, then construct ΔLMN and ΔABC
Draw the line segment AB = 5cm. From the point A draw a line segment AD = 6cm making an angle of 60° with AB. Draw a perpendicular bisector of AD. Select the correct figure.
The image of construction of A’C’B a similar triangle of ΔACB is given below. Then choose the correct option.
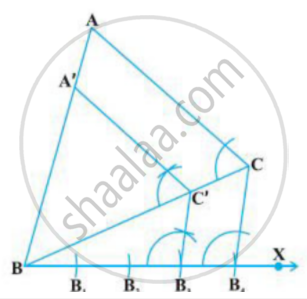
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

By geometrical construction, it is possible to divide a line segment in the ratio `sqrt(3) : 1/sqrt(3)`.
Draw a triangle ABC in which BC = 6 cm, CA = 5 cm and AB = 4 cm. Construct a triangle similar to it and of scale factor `5/3`.
