Advertisements
Advertisements
Question
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
Solution
ABCD is a square whose diagonals AC and BD intersect each other at right angles at O.
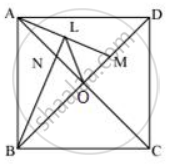
∠ BAM = ∠ BAO + ∠ OAM
⇒ ∠ BAM = `45° + (45°)/2 = 67 (1°)/2`
And
⇒ ∠ BMA = 180° - (∠ AOM + ∠ OAM)
⇒ ∠ BMA = 180° - 90° - `(45°)/2 = 90° - (45°)/2 = 67(1°)/2`
∴ ∠ BAM = ∠ BMA
APPEARS IN
RELATED QUESTIONS
How many tangents can a circle have?
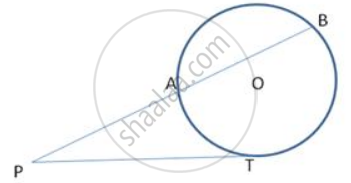
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
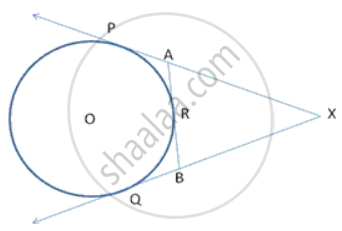
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
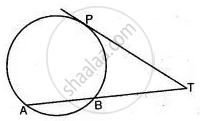
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.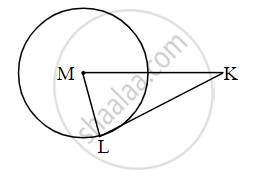
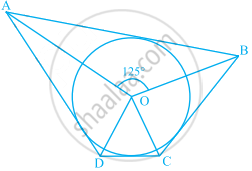
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

