Advertisements
Advertisements
Question
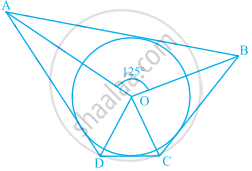
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
Options
62.5°
45°
35°
55°
Solution
In figure, if ∠AOB = 125°, then ∠COD is equal to 55°.
Explanation:

ABCD is a quadrilateral circumscribing the circle
We know that, the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
So, we have
∠AOB + ∠COD = 180°
125° + ∠COD = 180°
∠COD = 55°
APPEARS IN
RELATED QUESTIONS
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
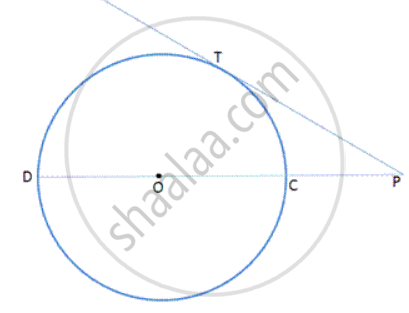
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
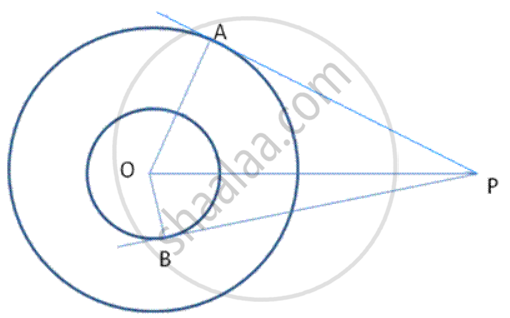
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
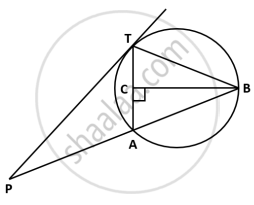
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
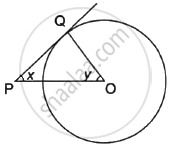
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.