Advertisements
Advertisements
Question
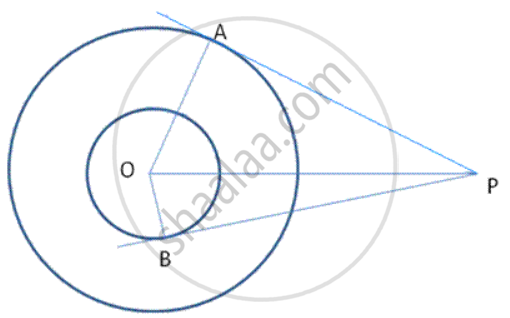
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
Solution
∠ OAP = ∠ OBP = 90° (radius is .l to tangent at the point of contact)
In right Δ OAP ,
OP2 = OA2 + AP2
OP2 = 52 + 122 = 25+ 144= 169
OP = 13 cm
In right Δ OBP,
OP2 = OS2 + BP2
BP2 = 132 -32
BP2 =169 - 9 = 160
BP = `4 sqrt 10` cm
APPEARS IN
RELATED QUESTIONS
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is ______
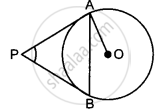
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
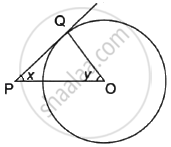
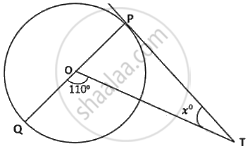
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.