Advertisements
Advertisements
Question
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
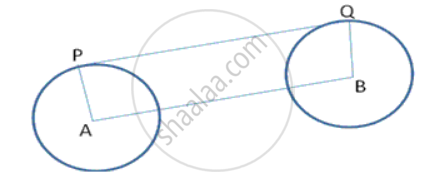
Solution
To find: PQ
R1 = 3cm, R2 = 8cm
AB= 13cm
PQ2 = AB2 -(R2 -R1)2
⇒ PQ2 = 132 - ( 8 - 3)2
⇒ PQ2 = 169 - 25
⇒ PQ2 = 144
⇒ PQ = 12cm
Length of direct common tangent is 12cm
APPEARS IN
RELATED QUESTIONS
A line intersecting a circle in two points is called a ______.
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
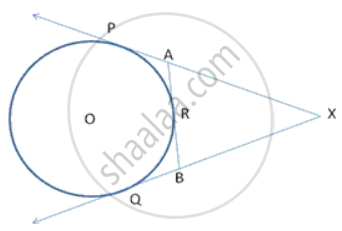
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
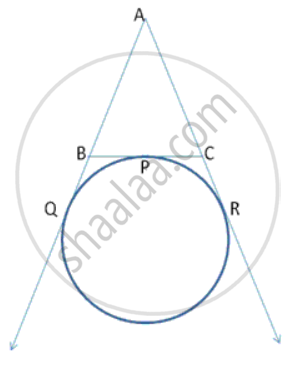
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
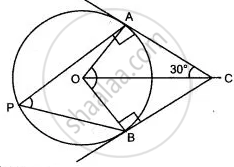
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
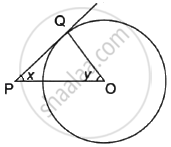
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?

In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is ______.
