Advertisements
Advertisements
Question
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
Solution

OA ⊥ AP (radius is perpendicular to tangent at the point of contact)
In right Δ OAP,
OP2 = OA2 + AP2
AP2 = 172 + 152
= 289 - 225
= 64
AP = 8
The radius of the circle is 8 cm.
APPEARS IN
RELATED QUESTIONS
A tangent to a circle intersects it in ______ point (s).
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)


In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.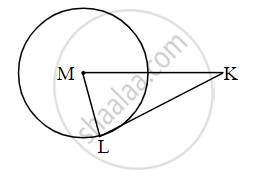
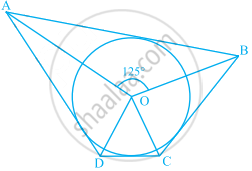
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
