Advertisements
Advertisements
प्रश्न
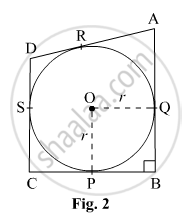
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
विकल्प
(A) 11
(B) 18
(C) 6
(D) 15
उत्तर
We know that, the lengths of the tangents drawn from an external point to a circle are equal.
DS = DR = 5 cm
∴ AR = AD − DR = 23 cm − 5 cm = 18 cm
AQ = AR = 18 cm
∴ QB = AB − AQ = 29 cm − 18 cm = 11 cm
QB = BP = 11 cm
In right Δ PQB, PQ2 = QB2 + BP2 = (11 cm)2 + (11 cm)2 = 2 × (11 cm)2
PQ = `11sqrt2r` cm … (1)
In right ΔOPQ,
PQ2 = OQ2 + OP2 = r2 + r2 = 2 r2
PQ = `11sqrt2r`… (2)
From (1) and (2), we get
r = 11 cm
Thus, the radius of the circle is 11 cm.
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
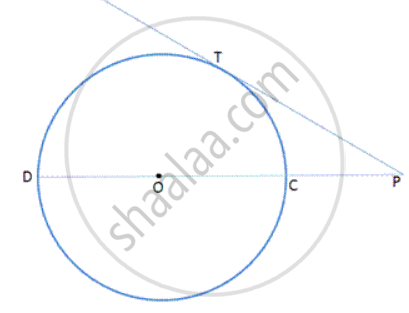
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
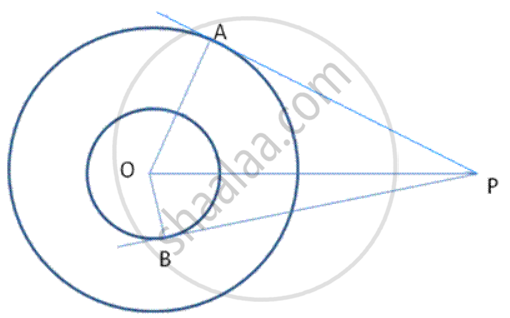
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

Tangents from an external point to a circle are ______
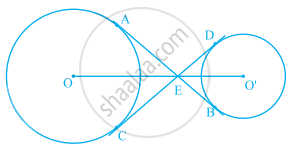
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.