Advertisements
Advertisements
प्रश्न
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
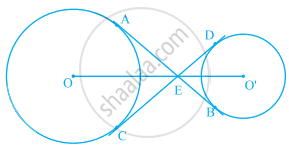
The common tangents AB and CD to two circles with centres O and O' intersect at E between their centres. Prove that the points O, E and O' are collinear.
उत्तर
Join AO, OC and O’D, O’B.
Now, in ∆EO’D and ∆EO’B,
O’D = O’B
O’E = O’E
ED = EB ...[Tangents drawn from an external point to the circle are equal in length]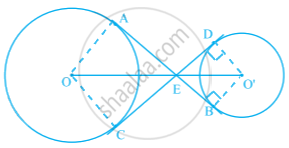
∴ EO’D ≅ ∆ EO’B ...[By SSS congruence criterion]
⇒ ∠O’ED = ∠O’EB ...(i)
i.e., O’E is the angle bisector of ∠DEB.
Similarly, OE is the angle bisector of ∠AEC.
Now, in quadrilateral DEBO’.
∠O’DE = ∠O’BE = 90° ...[CED is a tangent to the circle and O’D is the radius, i.e., O’D ⊥ CED]
⇒ ∠O’DE + ∠O’BE = 180°
∴ ∠DEB + ∠DO’B = 180° ...(ii) [∵ DEBO’ is cyclic quadrilateral]
Since, AB is a straight line.
∴ ∠AED + ∠DEB = 180°
⇒ ∠AED + 180° – ∠DO’B = 180° ...[From (ii)]
⇒ ∠AED = ∠DO’B ...(iii)
Similarly, ∠AED = ∠AOC ...(iv)
Again from equation (ii),
∠DEB = 180° – ∠DO’B
Dividing by 2 on both sides, we get
`1/2 ∠"DEB" = 90^circ - 1/2 ∠"DO'B"`
⇒ ∠DE'O = 90° `-1/2` ∠DO'B ...(v) [∵ O'E is the angle bisector of ∠DEB i.e. `1/2` ∠DEB = ∠DEO']
Similarly, ∠AEC = 180° – ∠AOC
Dividing by 2 on both sides, we get
`1/2 ∠"AEC" = 90^circ - 1/2 ∠"AOC"`
⇒ `∠"AEO" = 90^circ - 1/2 ∠"AOC"` ...(vi) [∵ OE is the angle bisector of ∠AEC i.e., `1/2 ∠"AEC" = ∠"AEO"`]
Now, ∠AED + ∠DEO' + ∠AEO = ∠AED + `(90^circ - 1/2 ∠"DO'B") + (90^circ - 1/2 ∠"AOC")`
= `∠"AED" + 180^circ - 1/2 (∠"DO'B" + ∠"AOC")`
= `∠"AED" + 180^circ - 1/2 (∠"AED" + ∠"AED")` ...[From equation (iii) and (iv)]
= `∠"AED" + 180^circ - 1/2 (2 xx ∠"AED")`
= ∠AED + 180° – ∠AED = 180°
∴ ∠AED + ∠DEO' + ∠AEO = 180°
So, OEO’ is straight line.
Hence, O, E and O’ are collinear.
संबंधित प्रश्न
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

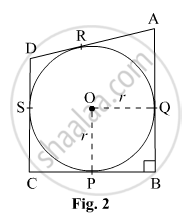
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
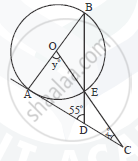
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

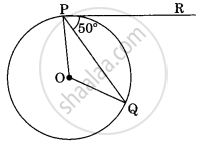
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
Tangents from an external point to a circle are ______
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

