Advertisements
Advertisements
प्रश्न
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
उत्तर
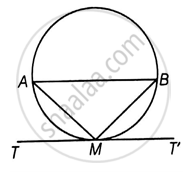
Let us draw a circle in which AMB is an arc and M is the mid-point of the arc AMB.
Joined AM and MB.
Also TT' is a tangent at point M on the circle.
To Prove: AB || TT'
Proof: As M is the mid point of Arc AMB
Arc AM = Arc MB
AM = MB ...[As equal chords cuts equal arcs]
∠ABM = ∠BAM ...[Angles opposite to equal sides are equal] [1]
Now, ∠BMT' = ∠BAM ...[Angle between tangent and the chord equals angle made by the chord in alternate segment] [2]
From [1] and [2]
∠ABM = ∠BMT'
So, AB || TT' ...[Two lines are parallel if the interior alternate angles are equal]
Hence Proved!
APPEARS IN
संबंधित प्रश्न
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
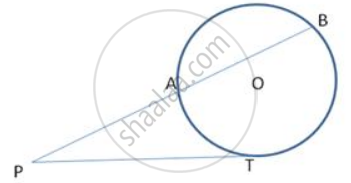
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = Scm, find PT.
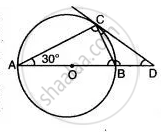
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
The distance between two parallel tangents of a circle of radius 4 cm is ______

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

