Advertisements
Advertisements
प्रश्न
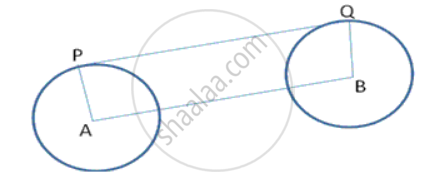
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

उत्तर
In the given figure, we have an external point X from where two tangents, XP and XQ, are drawn to the circle.
XP = XQ (The lengths of the tangents drawn from an external point to the circle are equal.)
Similarly, we have:
AP = AR
BQ = BR
Now, XP = XA + AP ...(1)
XQ = XB + BQ ...(2)
On putting AP = AR in equation (1) and BQ = BR in equation (2), we get:
XP = XA + AR
XQ = XB + BR
Since XP and XQ are equal, we have:
XA + AR = XB + BR
Hence, proved.
APPEARS IN
संबंधित प्रश्न
A tangent to a circle intersects it in ______ point (s).
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
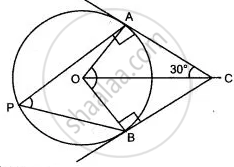
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
Find the value of ∠DCE.

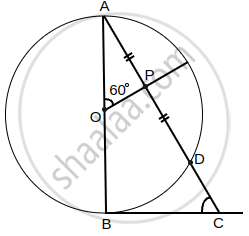
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
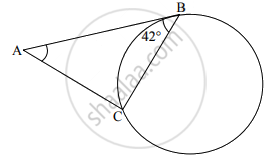
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
