Advertisements
Advertisements
प्रश्न
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
उत्तर
Let PA and PB be the two tangents drawn to the circle with centre O and radius a such that ∠APB=60°
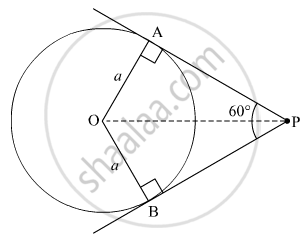
In ∆OPB and ∆OPA
OB = OA = a (Radii of the circle)
∠OBP = ∠OAP=90° (Tangents are perpendicular to radius at the point of contact)
BP = PA (Lengths of tangents drawn from an external point to the circle are equal)
So, ∆OPB ≌ ∆OPA (SAS Congruence Axiom)
∴ ∠OPB = ∠OPA=30° (CPCT)
Now,
In ∆OPB
`sin 30^@ = "OB"/"OP"`
`=> 1/2 = a/(OP)`
`=> OP= 2a`
Thus the length of OP is 2a
APPEARS IN
संबंधित प्रश्न
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
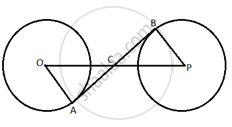
The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
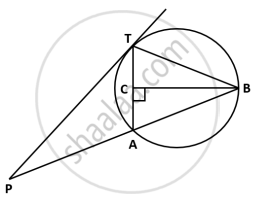
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.