Advertisements
Advertisements
प्रश्न
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
उत्तर
In ΔAOC, ACO = 30° (Given)

∠OAC = 90° [radius is perpendicular to the tangent at the point of contact]
By angle sum property, ACO + OAC + AOC = 180o
AOC = 180° – (90° + 30°) = 60°
Consider Δ AOC and Δ BOC
AO = BO (radii)
AC = BC (tangents to a circle from an external point are equal in length)
OC = OC (Common)
ΔAOC ≅ ΔBOC
1) ∠BCO = ∠ACO = 30°
2) ∠AOC = ∠BOC = 60°
∠AOB = ∠AOC + ∠BOC = 120°
3) We know that, “If two angles stand on the same chord, then the angle at the centre is twice the angle at the circumference.
∠AOB and ∠APB stand on the same chord AB.
∠AOB = 2∠APB
So ∠APB = 1/2 ∠AOB = 60°
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
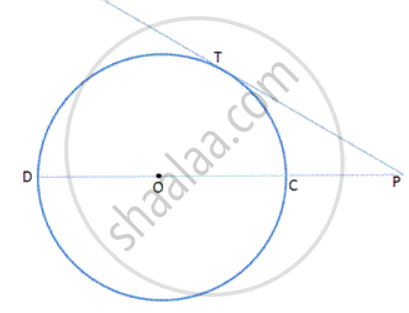
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

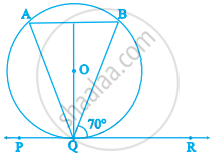
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to ______.
The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
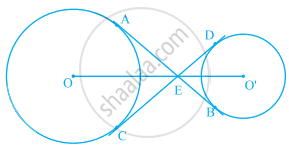
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
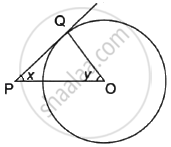
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
