Advertisements
Advertisements
प्रश्न
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
उत्तर
Given: Chord PQ is parallel to tangent at R.
To prove: R bisects the arc PRQ.
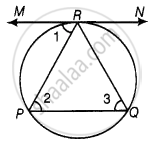
Proof: ∠1 = ∠2 ...[Alternative interior angles]
∠1 = ∠3 ...[Angle between tangent and chord is equal to angle made by chord in alternative segment]
∴ ∠2 = ∠3
⇒ PR = QR ...[Sides opposite to equal angles are equal]
⇒ PR = QR
So, R bisects PQ.
संबंधित प्रश्न
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
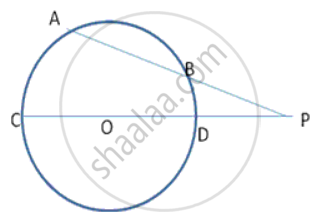
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
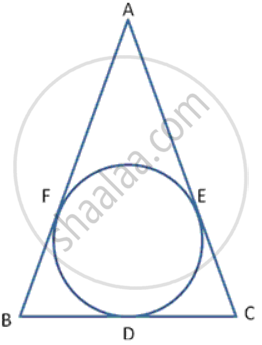
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
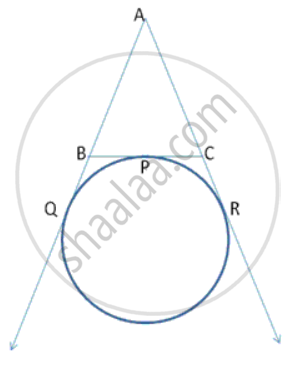
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

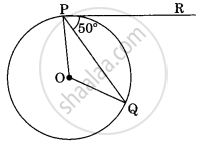
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
