Advertisements
Advertisements
प्रश्न
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.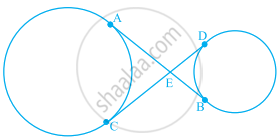
उत्तर
Given: Common tangents AB and CD to two circles intersecting at E.
To prove: AB = CD

Proof: EA = EC ...(i) [The length of tangents drawn from an internal point to a circle are equal]
And
EB = ED ...(ii) [The length of tangents drawn from an internal point to a circle are equal]
On adding equations (i) and (ii), we get
EA + EB = EC + ED
⇒ AB = CD
Hence proved.
APPEARS IN
संबंधित प्रश्न
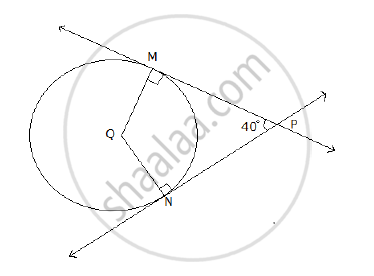
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
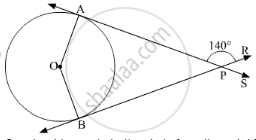
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
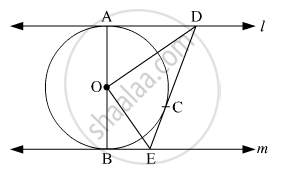
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
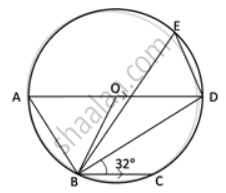
Find: ∠BED
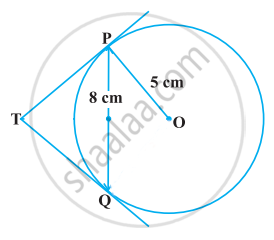
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
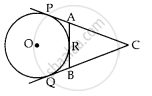
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the center O at a point Q such that OQ = 13 cm. Length PQ is ______
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
