Advertisements
Advertisements
Question
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.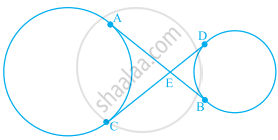
Solution
Given: Common tangents AB and CD to two circles intersecting at E.
To prove: AB = CD

Proof: EA = EC ...(i) [The length of tangents drawn from an internal point to a circle are equal]
And
EB = ED ...(ii) [The length of tangents drawn from an internal point to a circle are equal]
On adding equations (i) and (ii), we get
EA + EB = EC + ED
⇒ AB = CD
Hence proved.
APPEARS IN
RELATED QUESTIONS
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
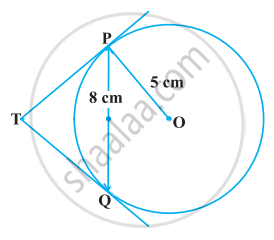
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
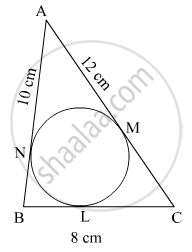
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
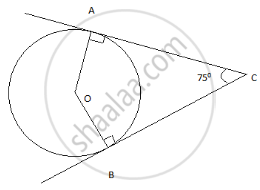
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
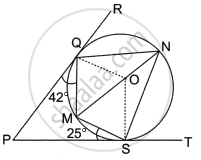
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
