Advertisements
Advertisements
प्रश्न
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
उत्तर १
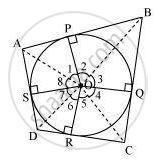
Let ABCD be a quadrilateral circumscribing a circle centred at O such that it touches the circle at point P, Q, R, and S. Let us join the vertices of the quadrilateral ABCD to the centre of the circle.
Consider ΔOAP and ΔOAS,
AP = AS .....(Tangents from the same point)
OP = OS ..... (Radii of the same circle)
OA = OA ....(Common side)
ΔOAP ≅ ΔOAS .... (SSS congruence criterion)
Therefore, A ↔ A, P ↔ S, O ↔ O
And thus, ∠POA = ∠AOS
∠1 = ∠8
Similarly,
∠2 = ∠3
∠4 = ∠5
∠6 = ∠7
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360º
(∠1 + ∠8) + (∠2 + ∠3) + (∠4 + ∠5) + (∠6 + ∠7) = 360º
2∠1 + 2∠2 + 2∠5 + 2∠6 = 360º
2(∠1 + ∠2) + 2(∠5 + ∠6) = 360º
(∠1 + ∠2) + (∠5 + ∠6) = 180º
∠AOB + ∠COD = 180º
Similarly, we can prove that ∠BOC + ∠DOA = 180º
Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
उत्तर २
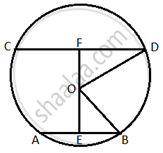
Let ABCD be a quadrilateral circumscribing a circle with centre at O.
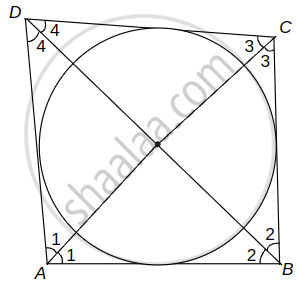
Join OA, OB, OC and OD.
Here, Let ∠DAO = ∠BAO = ∠1 ...[∵ AB and AD are tangents]
Similarly, ∠ABO = ∠CBO = ∠2 ...[∵ BA and BC are tangents]
And Let ∠BCO = ∠DCO = ∠3 ...[∵ CB and CD are tangents]
And Let ∠CDO = ∠ADO = ∠4 ...[∵ DC and DA are tangents]
Sum of all angles at the centre is 360°.
Also, the sum of the angles in quadrilateral, ABCD = 360°
∴ 2(∠1 + ∠2 + ∠3 + ∠4) = 360°
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 180° ...(i)
Now, In ΔAOB,
∠AOB = 180° – (∠1 + ∠2) ...(ii)
In ΔCOD, ∠COD = 180° – (∠3 + ∠4) ...(iii)
On adding equations (ii) and (iii), we get
∠AOB + ∠COD = 360° – (∠1 + ∠2 + ∠3 + ∠4)
= 360° – 180°
= 180° ... [From equation (i)]
Since AB and CD subtend supplementary angles at O.
Thus, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
APPEARS IN
संबंधित प्रश्न
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In the given figure PA = 6, PB = 4 and PC = 8. Find PD
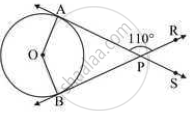
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
The number of tangents drawn at a point of the circle is/are ______
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is ______
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
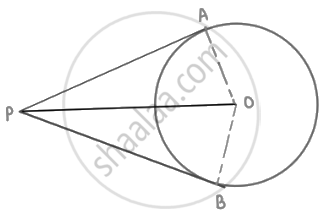
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

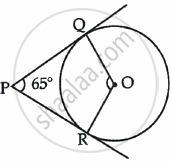
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
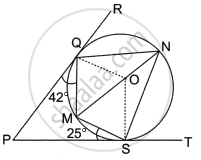
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
