Advertisements
Advertisements
प्रश्न
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
उत्तर

Step of construction
Step I - First of all, we draw a circle of radius AB = 4 cm.
Step II - Mark a point P from the centre at a distance of 6 cm from the point O.
Step III - Draw a right bisector of OP, intersecting OP at Q.
Step IV - Taking Q as centre and radius OQ = PQ, draw a circle to intersect the given circle at T and T’.
Step V - Join PT and PT’ to obtain the required tangents.
Thus, PT and PT' are the required tangents.
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
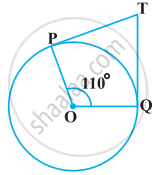
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
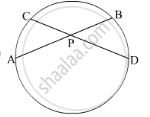
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
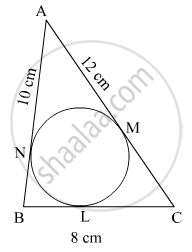
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
The length of the tangent from an external point on a circle is ______
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
