Advertisements
Advertisements
प्रश्न
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
उत्तर
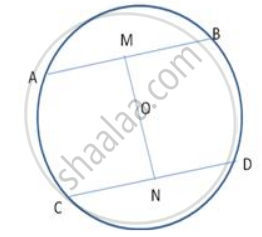
AM = MB
CN = ND
∴ OM ⊥ AB
and ON ⊥ CD
(A line bisecting the chord and passing through the centre of the circle is perpendicular to the chord)
∴ ∠ OMA = ∠ OND = 90° each
But these are alternate interior angles
∴ AB || CD
APPEARS IN
संबंधित प्रश्न
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
Find the area of the shaded region in Fig. 8, where \\

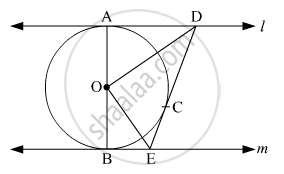
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
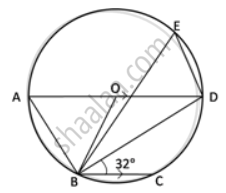
Find: ∠BED
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
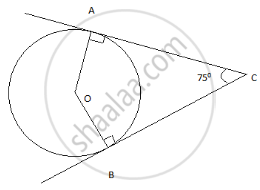
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
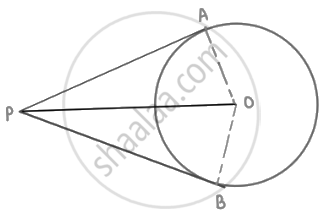
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.