Advertisements
Advertisements
प्रश्न
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
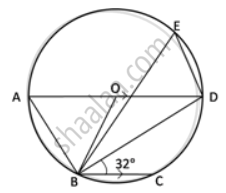
Find: ∠BED
उत्तर
In Δ OAB ,
OA = OB ...(Radii of the same circle° )
⇒ ∠ OAB = ∠ OBA = x (say)
⇒ ∠ OAB + ∠ OBA + ∠ AOB = 180°
⇒ x + x + 64° = 180°
⇒ 2x = 180 ° - 64 °
⇒ 2x = 116°
⇒ x = 58°
⇒ ∠ OAB = 58°
i.e. ∠ DAB = 58°
⇒ ∠ DAB = ∠BED = 58° ....(Angles inscribed in the same arc are equal)
APPEARS IN
संबंधित प्रश्न
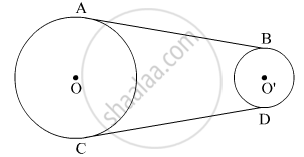
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7 : 19 ?
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is ______
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

