Advertisements
Advertisements
प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

उत्तर
i. ∠DAE = 70° ...(Given)
∠BAD + ∠DAE = 180° ...(Linear pair)
Since ABCD is a cyclic quadrilateral, sum of the measures of the opposite angles are supplementary.
So, ∠BCD + ∠BAD = 180°
ii. ∠BOD = 2∠BCD ...(Inscribed angle theorem)
iii. In ΔOBD
OB = OD ...(Radii of same circle)
By angle sum property,
∠OBD + ∠ODB + ∠BOD = 180°
APPEARS IN
संबंधित प्रश्न
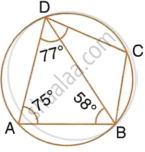
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
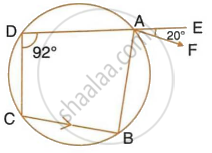
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
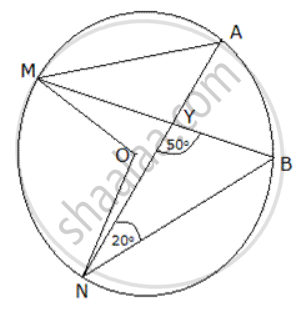
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

