Advertisements
Advertisements
प्रश्न
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
उत्तर
Let QR be a chord in a circle with center O and ∠1 and ∠2 are the angles made by tangent at point R and Q with chord respectively.
To Prove: ∠1 = ∠2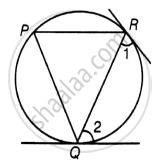
Let P be another point on the circle, then, join PQ and PR.
Since, at point Q, there is a tangent.
∠RPQ = ∠2 ...[Angles in alternate segments are equal] [Equation 1]
Since, at point R, there is a tangent.
∠RPQ = ∠1 ...[Angles in alternate segments are equal] [Equation 2]
From equation 1 and equation 2
∠1 = ∠2
Hence Proved.
APPEARS IN
संबंधित प्रश्न
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

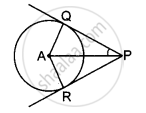
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
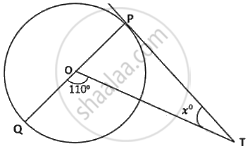
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.