Advertisements
Advertisements
प्रश्न
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
उत्तर
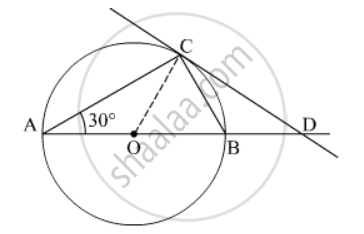
It is given that ∠BAC = 30° and AB is diameter.
∠ACB = 90° ...(Angle formed by the diameter is 90°)
In ∆ABC,
∠ACB + ∠BAC + ∠ABC = 180°
⇒ 90° + 30° + ∠ABC = 180°
⇒ ∠ABC = 60°
⇒ ∠CBD = 180° – 60° = 120° ...(∠CBD and ∠ABC form a linear pair)
In ∆OCD,
∠OCD = 90° ...(Angle made by Radius on the tangent)
∠OBC = ∠ABC = 60°
Since OB = OC,
∠OCB = ∠OBC = 60° ...(OC = OB = radius)
In ∆OCB,
⇒ ∠COB + ∠OCB + ∠OBC = 180°
⇒ ∠COB + 60° + 60° = 180°
⇒ ∠COB = 60°
In ∆OCD,
∠COD + ∠OCD + ∠ODC = 180°
⇒ 60° + 90° + ∠ODC = 90° ...(∠COD = ∠COB)
⇒ ∠ODC = 30°
In ∆CBD,
∠CBD = 120°
∠BDC = ∠ODC = 30°
⇒ ∠BCD + ∠BDC + ∠CBD = 180°
⇒ ∠BCD + 30° + 120° = 180°
⇒ ∠BCD + 30° = ∠BDC
Angles made by BC and BD on CD are equal, so ∆CBD is an isosceles triangle and therefore, BC = BD.
संबंधित प्रश्न
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
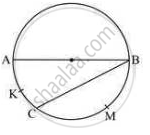
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
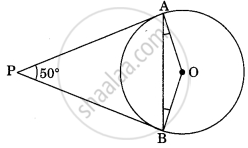
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
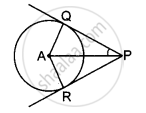
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

