Advertisements
Advertisements
प्रश्न
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]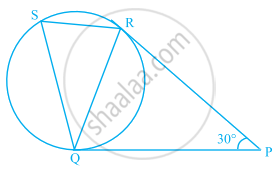
उत्तर
PQ and PR are two tangents drawn from an external point P.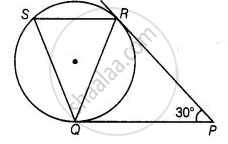
∴ PQ = PR ...[The length of tangents drawn from an external point to a circle are equal]
⇒ ∠PQR = ∠QRP ...[Angles opposite to equal sides are equal]
Now, In ΔPQR,
∠PQR + ∠QRP + ∠RPQ = 180° ...[Sum of all interior angles of any triangle is 180°]
⇒ ∠PQR + ∠PQR + 30° = 180°
⇒ 2∠PQR = 180° – 30° = 150° ...[∵ ∠PQR = ∠QRP]
⇒ ∠PQR = `(180^circ - 30^circ)/2` = 75°
Since, SR || QP
∴ ∠SRQ = ∠RQP = 75° ...[Alternative interior angles]
Also, ∠PQR = ∠QSR = 75° ...[By alternative segment theorem]
In ΔQRS,
∠Q + ∠R + ∠S = 180° ...[Sum of all interior angles of any triangles is 180°]
⇒ ∠Q = 180° – (75° + 75°) = 30°
∴ ∠RQS = 30°
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
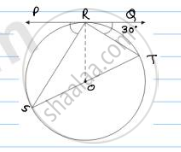
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.
What is the area of a semi-circle of diameter ‘d’?
