Advertisements
Advertisements
प्रश्न
What is the area of a semi-circle of diameter ‘d’?
पर्याय
`1/16 πd^2`
`1/4 πd^2`
`1/8 πd^2`
`1/2 πd^2`
उत्तर
`bb(1/8 πd^2)`
Explanation:
As we know that,
Area of semi-circle = `(πr^2)/2`
and radius (r) = `("Diameter" (d))/2`
∴ r = `d/2`
Thus, area of semi-circle = `π/2(d/2)^2`
= `(πd^2)/(2 xx 4)`
= `(πd^2)/8`
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

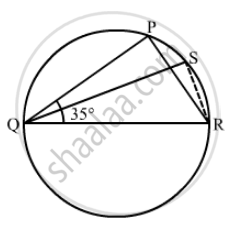
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
The greatest chord of a circle is called its
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
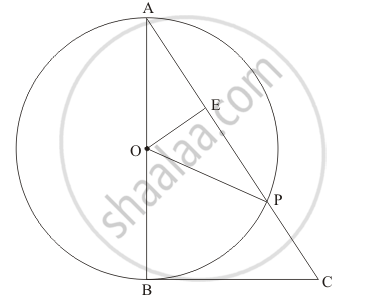
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

