Advertisements
Advertisements
प्रश्न
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

उत्तर
The given figure is below
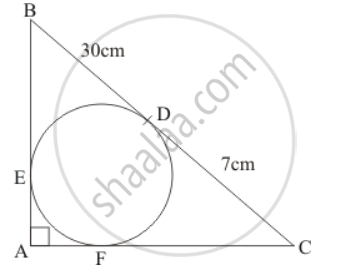
(i) The given triangle ABC is a right triangle where side BC is the hypotenuse. Let us now apply Pythagoras theorem. We have,
`AB^2+AC^2=BC^2`
Looking at the figure we can rewrite the above equation as follows.
`(BE+EA)^2+(AF+FC)^2=(30+7)^2` …… (1)
From the property of tangents we know that the length of two tangents drawn from the same external point will be equal. Therefore we have the following,
BE = BD
It is given that BD = 30 cm. Therefore,
BE = 30 cm
Similarly,
CD = FC
It is given that CD = 7 cm. Therefore,
FC = 7 cm
Also, on the same lines,
EA = AF
Let us substitute these in equation (1). We get,
`(BE+EA)^2+(AF+FC)^2=(30+7)^2`
`(30+AF)^2+(AF+7)^2=37^2`
`(30^2+2 xxAF+AF^2)+(AF^2+2xx7xxAF+7^2)=1369`
`900+60AF+AF^2+AF^2+14AF+49=1369`
`2F^2+74AF-420=0`
`AF^2+37AF-210=0`
`AF^2(AF+42)-5(AF+42)=0`
`AF(AF+42)-5(AF+42)=0`
`(AF-5)(AF+42)=0`
Therefore,
Therefore,
AF = 5
Or,
AF = − 42
Since length cannot have a negative value,
AF = 5
APPEARS IN
संबंधित प्रश्न
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
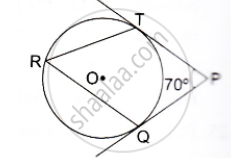
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
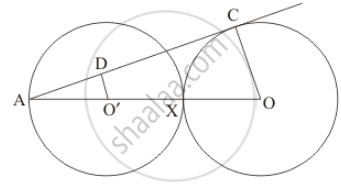
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
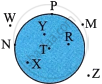 |
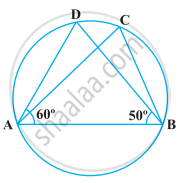
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.