Advertisements
Advertisements
Question
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
Solution
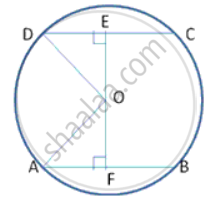
AF = FB = 8.4 cm
And DE = EC ----(1)
(Perpendicular from centre to a chord bisects the chord)
In right Δ ODA,
By Pythagoras theorem, OA2 = OF2 + AF2
= (11.2)2 + (8.4)2
= 125.44 + 70.56
OA2 = 196
OA = 14 cm
OA = OD = 14cm (radii of same circle)
Similarly, In Δ DEO
OD2 = OE2 + DE2
DE2 = 142 + 8.42
= 196 - 70.56
DE2 = 125.44
DE = 11.2 cm
∴ length of chord DC = 2DE = 2(11.2) = 22.4 cm
APPEARS IN
RELATED QUESTIONS
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

Tangents from an external point to a circle are ______
Find the value of ∠DCE.

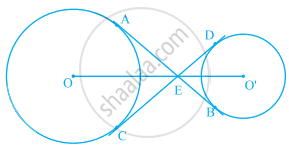
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.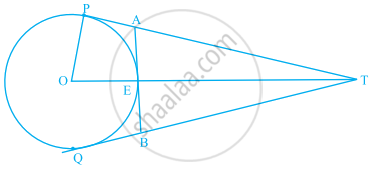
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

