Advertisements
Advertisements
Question
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
Solution
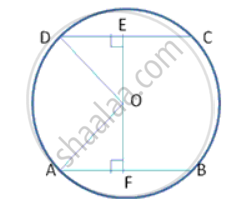
AF = FB = 3cm
CE = ED = 7.2cm
(Perpendicular from centre to a chord bisects the chord)
In right Δ AFO, By Pythagoras theorem,
OA2 =OF2+ AF2
OA2 = (7.2)2 + (3)2
OA2 = 51.84 + 9
OA2 = 60.84
OA = 7.8cm
OA = OC = 7.8cm (radii of same circle)
Similarly, In right Δ OFC,
OC2 = OE2 + EC2
OE2 = (7 .8)2 - (7.2)2
= 60.84 - 51.84
OE2 = 9
OE = 3cm
Distance from centre of chord CD with length 14.4cm is 3cm.
APPEARS IN
RELATED QUESTIONS
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ______.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
Find the area of a sector of a circle of radius 28 cm and central angle 45°.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
The area of the sector of a circle of radius 12 cm is 60π cm2. The central angle of this sector is ______.
