Advertisements
Advertisements
Question
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
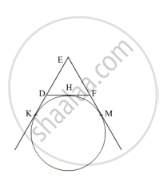
Options
A. 18
B. 13.5
C. 12
D. 9
Solution
EK = 9 cm
As length of tangents drawn from an external point to the circle are equal.
∴EK = EM = 9 cm
Also, DH = DK and FH = FM … (i)
EK = EM = 9 cm
⇒ ED + DK = 9 cm and EF + FM = 9 cm
⇒ ED + DH = 9 cm and EF + HF = 9 cm [From equation (i)] … (ii)
Perimeter of ΔEDF = ED + DF + EF
= ED + DH + HF + EF
= (9 + 9) cm [From equation (ii)]
= 18 cm
Hence, the correct option is A.
RELATED QUESTIONS
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
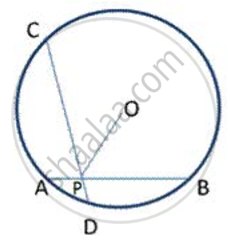
Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.
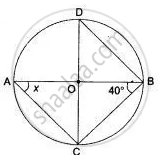
If O is the centre of the circle, find the value of x in each of the following figures
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
