Advertisements
Advertisements
Question
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
Solution
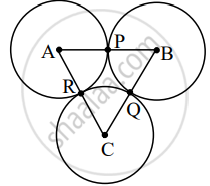
Given: AB = 36, BC = 32, CA = 30
To Find: Radii of each circle.
Solution:
Let x, y, z be the radii of the circles with centers A, B, C respectively.
∴ AP = RA = x, PB = BQ = y, CR = QC = z
AB = AP + PB ....[A–P–B]
∴ 36 = x + y ...(ii) [From (i) and given]
BC = BQ + QC ....[B – Q – C]
∴ 32 = y + z .....(iii) [From (i) and given]
CA = CR + RA ......[C – R – A]
∴ 30 = z + x ......(iv) [From (i) and given]
Now,
AB + BC + CA = 36 + 32 + 30
∴ (AP + PB) + (BQ + QC) + (CR + RA) = 98 ......[A–P–B, B–Q–C, C–R–A]
∴ (x + y) + (y + z) + (z + x) = 98 ......[From (i)]
∴ 2x + 2y + 2z = 98
∴ 2(x + y + z) = 98
∴ x + y + z = `98/2`
∴ x + y + z = 49
∴ (x + y) + z = 49 .....[From (ii)]
∴ 36 + z = 49
∴ z = 49 – 36
∴ z = 13 ......(v)
y + z = 32 ......[From (iii)]
∴ y + 13 = 32 ......[From (v)]
∴ y = 32 – 13
∴ y = 19
z + x = 30 .....[From (iv)]
∴ 13 + x = 30 .....[From (v)]
∴ x = 30 – 13
∴ x = 17
APPEARS IN
RELATED QUESTIONS
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
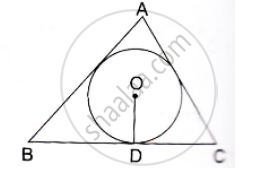
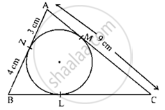
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

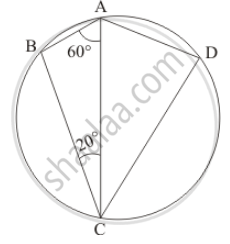
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.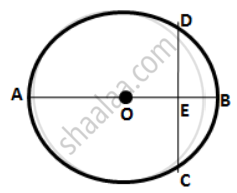
The diameter of a circle is 12.6 cm. State, the length of its radius.
Draw circle with the radii given below.
2 cm
A part of circumference of a circle is called as _______
A line segment with its end points on the circle is called a ______________
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
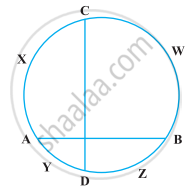
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
Is every chord of a circle also a diameter?
The circumcentre of a triangle is the point which is ______.
