Advertisements
Advertisements
प्रश्न
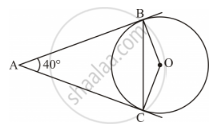
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
विकल्प
40°
50°
140°
150°
उत्तर
It is known that the tangent is perpendicular to the radius through the point of contact.
∴ ∠ABO = ∠ACO = 90°
Using angle sum property in quadrilateral ABOC:
∠ABO + ∠BOC + ∠ACO + ∠BAC = 360°
⇒ 90° + ∠BOC + 90° + 40° = 360°
⇒ ∠BOC + 220° = 360°
⇒ ∠BOC = 360° - 220° = 140°
APPEARS IN
संबंधित प्रश्न
A circle can have ______ parallel tangents at the most.
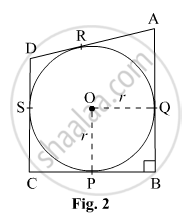
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
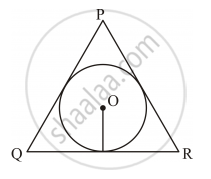
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.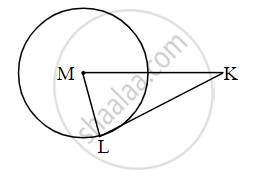
Find the value of ∠DCE.


In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
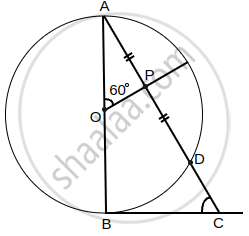
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.