Advertisements
Advertisements
प्रश्न
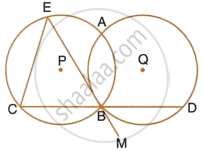
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
उत्तर
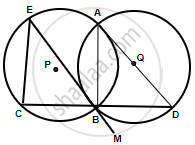
Join AB and AD
EBM is a tangent and BD is a chord.
∠DBM = ∠BAD ...(Angles in alternate segments)
But, ∠DBM = ∠CBE ...(Vertically opposite angles)
∴ ∠BAD = ∠CBE
Since in the same circle or congruent circles, if angles are equal, then chords opposite to them are also equal.
Therefore, CE = BD
APPEARS IN
संबंधित प्रश्न
In the following figure; If AB = AC then prove that BQ = CQ.

From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

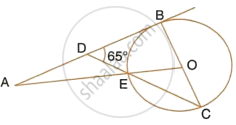
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
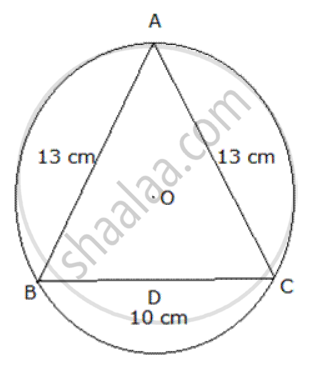
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
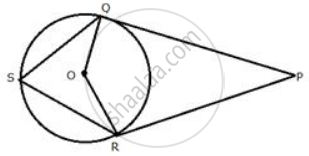
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.