Advertisements
Advertisements
प्रश्न
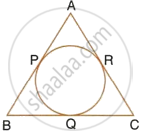
In the following figure; If AB = AC then prove that BQ = CQ.

उत्तर
Since, from A, AP and AR are the tangents to the circle
Therefore, AP = AR
Similarly, we can prove that
BP = BQ and CR = CQ
Adding,
AP + BP + CQ = AR + BQ + CR
(AP + BP) + CQ = (AR + CR) + BQ
AB + CQ = AC + BQ
But AB = AC
Therefore, CQ = BQ or BQ = CQ
APPEARS IN
संबंधित प्रश्न
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

