Advertisements
Advertisements
प्रश्न
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

उत्तर
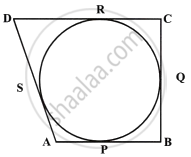
Let the circle touch the sides AB, BC, CD and DA of quadrilateral ABCD at P, Q, R and S respectively.
Since AP and AS are tangents to the circle from external point A
AP = AS ...(i)
Similarly, we can prove that:
BP = BQ ...(ii)
CR = CQ ...(iii)
DR = DS ...(iv)
Adding,
AP + BP + CR + DR = AS + DS + BQ + CQ
AB + CD = AD + BC
Hence, AB + CD = AD + BC
APPEARS IN
संबंधित प्रश्न
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
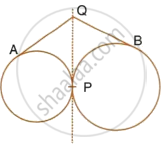
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
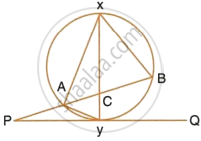
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
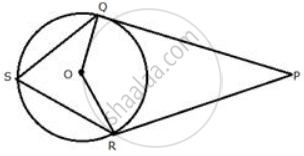
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
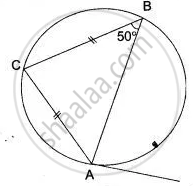
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

