Advertisements
Advertisements
प्रश्न
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
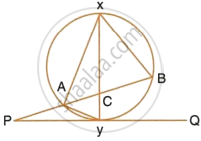
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
उत्तर
In the above figure,
XY is a diameter of the circle PQ is tangent to the circle at Y.
∠AXB = 50° and ∠ABX = 70°
i. In ΔAXB,
∠XAB + ∠ABX + ∠AXB = 180° ...(Angles of a triangle)
`=>` ∠XAB + 70° + 50° = 180°
`=>` ∠XAB + 120° = 180°
`=>` ∠XAB = 180° – 120° = 60°
But, ∠XAY = 90° ...(Angle in a semicircle)
∴ ∠BAY = ∠XAY – ∠XAB
= 90° – 60°
= 30°
ii. Similarly ∠XBY = 90° ...(Angle in a semicircle)
And ∠CXB = 70°
∴ ∠PBY = ∠XBY – ∠XBA
= 90° – 70°
= 20°
∴ ∠BYA = 180° – ∠AXB ...(∵ ∠BYA + ∠AYB = 180°)
= 180° – 50°
= 130°
∠PYA = ∠ABY ...(Angles in the alternate segment)
∠PBY = 20°
And ∠PYB = ∠PYA + ∠AYB
= 20° + 130°
= 150°
∴ ∠APY = 180° – (∠PYA + ∠ABY)
= 180° – (150° + 20°)
= 180° – 170°
= 10°
APPEARS IN
संबंधित प्रश्न
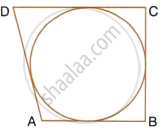
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
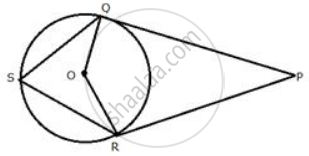
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
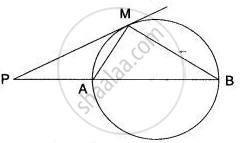
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
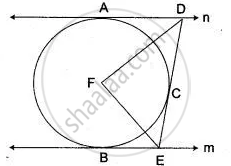
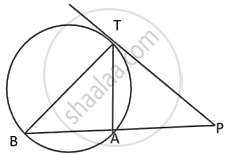
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.